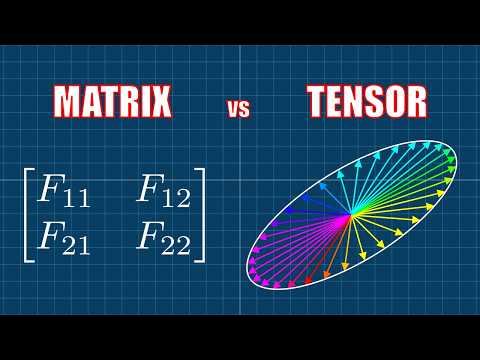
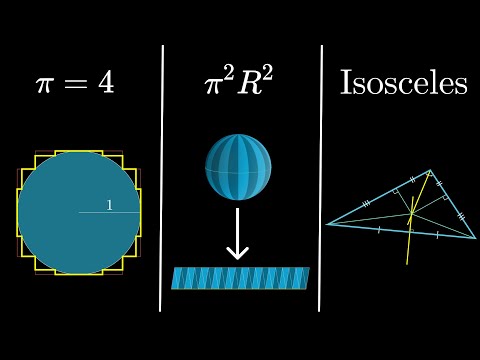
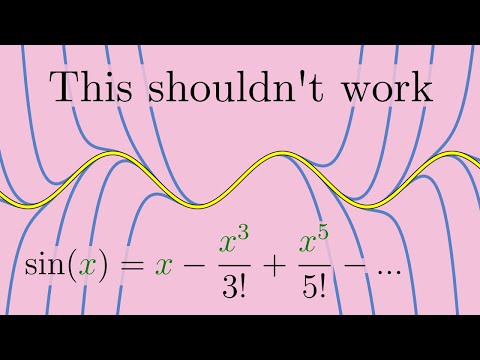
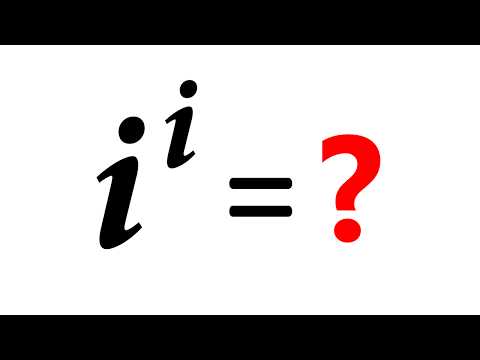This is my entry into the Second Summer of Math Exposition. I used to wonder about these questions ever since my first year in university, so in a sense this is a rather personal subject for me. I hope that this video reaches someone else who is also wondering about these issues. Here's the Desmos document for visualizing the n complex roots of any complex number: Videos mentioned in order of apparition: e to the pi i, a nontraditional take (old version) The 'Everything' Formula - Numberphile Winding numbers and domain coloring The 5 ways to visualize complex functions | Essence of complex analysis #3 Visualizing Complex-Valued Functions Jeff Tupper's webpage on the graph of x^x A relevant Stack Exchange question and answer that touches on these ideas: Chapters: 00:00 Intro and problem motivation 01:49 The R-to-C graph of x^a 04:37 The R-to-C graph of a^x 06:37 Rotations in complex exponentiation 07:27 The R-to-C graph of x^x 08:17 An alternative version of the graph of x^x 12:37 Recap of the various graphs of x^x 13:49 Homework 14:09 Summary and outro Music by Vincent Rubinetti Download the music on Bandcamp: Stream the music on Spotify: